Research Unit A: Quantum Information Theory
Quantum Information Theory develops new software architectures, algorithms, and experimental protocols for quantum simulators and quantum computers to extend their reach into different fields of science and technology. At the same time, it aims to achieve a universal description of entanglement in many-body systems.
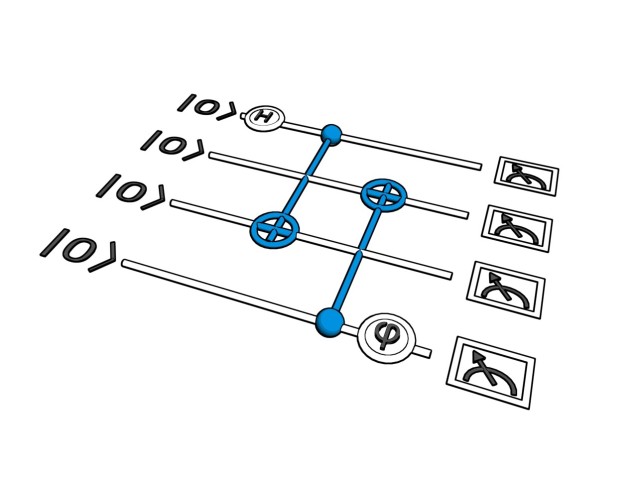
The area of Quantum Information pursues new ways of processing and transmitting information using the rules of Quantum Physics.
With the help of the superposition principle and entangled states, it became possible to devise protocols for communication that are immune to eavesdroppers or to construct algorithms that can solve problems which classical supercomputers will never be able to address. Other applications include the production of sensors able to detect ultra-weak signals, and of extraordinarily precise clocks.
In the last twenty years, a new field of research has emerged that aims to formulate a theory, akin to the classical information theory developed in the last century, capable of constructing the basis of future quantum devices.
This quantum information theory is much richer and more complex than its classical counterpart. Moreover, it is inherently interdisciplinary in nature, since it touches on multiple fields and brings physicists, computer scientists, and mathematicians together on common goals. It is far from being completed but has already found application areas well beyond the processing and transmission of information. In particular, it provides a new perspective to investigate, characterize, and classify the complex behaviour of large quantum systems, ranging from materials to chemical compounds, high energy problems, and even black holes or holographic principles.
Munich scientists have strongly contributed to the development of Quantum Information Theory during the last twenty years. Their expertise spreads out from pure mathematics over theoretical physics and chemistry to engineering. This will enable this research unit (RU-A) to address very ambitious goals with a very high potential impact in this and other research areas within MCQST Cluster of Excellence.
To achieve its main goals, collaborations and partnerships between theorists and experimentalists will allow RU-A to formulate relevant problems that, in a collaboration between physicists, mathematicians, electrical engineers, and computer scientists, will be solved by combining physical intuition with mathematical rigor.
RU-A Coordinators
Active Members in RU-A
